Formel Zur Berechnung Der Geschwindigkeit

This page in English language: Formulas for Speed, Acceleration, Time & Altitude

Auf dieser Seite finden Sie alle Formeln für dice Berech­nung von Geschwin­dig­keit, Beschleu­nigung, Weg und Zeit mit bzw. ohne An­fangs­geschwindig­keit. Ganz am Ende der Seite gibt es zum besseren Ver­ständnis der Formeln ein kleines Beispiel , indem die benötigte Zeit, die Be­schleu­nigung, die End­geschwindig­keit und dice Durch­schnitts­geschwindig­keit berechnet werden.

Links zu Unterseiten:

• Rechner für Weg, Ge­schwin­dig­keit, Be­schleu­nigung und Zeit – kons­tante Exist­schleu­nigung (Brems­weg­rechner)
• Beschleunigungsrechner
• Rechner für Durchschnitts­geschwin­dig­keit
• Weg, Ge­schwin­dig­keit, Be­schleu­nigung und Ruck: weitere Infos, Her­leitungen & Bei­spiele

Inhaltsverzeichnis

• Formeln für dice durch­schnitt­liche Ge­schwin­dig­keit
• Bedeutung der Variablen
• Vereinfachte Schreibweise dieser Formeln
• Formeln für die durch­schnitt­liche Beschleunigung
• Bedeutung der Variablen
• Hinweise zu den Formeln und speziell zu Differenzen
• Formeln bei gleich­mäßiger Be­schleu­nigung – Anfangs­geschwin­dig­keit = 0
• Formeln bei gleich­mäßiger Be­schleu­ni­gung – An­fangs­geschwin­dig­keit ≠ 0
• Beispiel mit Anfangsweg s₀
• Einfaches Beispiel
• Momentan­geschwin­dig­keit & Momentan­be­schleu­nigung
• Die wichtigsten Formeln
• Bedeutung der Variablen

Werbung

Formeln für die durch­schnitt­liche Ge­schwin­dig­keit

Mit den folgenden Formeln können die Durch­schnitts­ge­schwindig­keit v, der zurück­gelegte Weg due south oder die benötigte Zeit t berech­internet werden, wobei die durch­schnittliche (= mittlere) Ge­schwin­dig­keit v konstant ist. Diese Formeln mit den Delta­zeichen Δ stellen dice mathe­matisch korrekte Schreib­weise dar; die erste Formel wird auch Differenzen­quotient genannt, da dice Differenz der Wege durch die Zeit­differenz divi­diert wird. Frequently lässt man das Delta­zeichen jedoch weg, siehe die verein­fachten Formeln im über­nächsten Abschnitt.

$$five=\frac{\Delta s}{\Delta t}=\frac{s(t_1)-s(t_0)}{t_1-t_0}=\frac{s_1-s_0}{t_1-t_0}=\frac{zurückgelegter\ Weg}{benötigte\ Zeit}$$

$$\Delta s= v·\Delta t\qquad \Delta t =\frac{\Delta south}{v}$$

Bedeutung der Variablen

v	konstante Durchschnittsgeschwindigkeit in m/southward im Intervall [t0; t1] (Englisch velocity , daher dice Abkürzung v)
s bzw. Δs	zurückgelegter Weg bzw. Strecke (= Wegdifferenz) in yard im Intervall [t0; ti]
t bzw. Δt	benötigte Zeit (= Zeitdifferenz) in s (Englisch time , daher die Abkürzung t)
south( t0) bzw. s0	Weg zum Zeitpunkt t0 (Ausgangsort bzw. Anfangsweg); southward0 und t0 sind oft 0
south( t1) bzw. s1	Weg zum Zeitpunkt t1 (Zielort)

Den Differenzenquotienten und damit dice mittlere Geschwindigkeit kann human auch mit diesem Rechner bestimmen:

• Rechner zur Bestimmung der Durchschnitts­geschwin­digkeit

Vereinfachte Schreibweise dieser Formeln

Die obigen Formeln sind auch in einer ver­ein­fachten Schreib­weise bekannt. Aller­dings muss human be­denken, dass es sich bei Weg und Zeit um Differenzen handelt, siehe auch die folgenden Bei­spiele auf dieser Seite:

• Beispiel mit Anfangsweg s₀ ≠ 0 (Weg­differenz)
• Beispiel mit Anfangs­zeit t₀ ≠ 0 (Zeit­differenz)

Diese Tat­sache kann human being aber ignorieren, wenn der An­fangs­weg s₀ und die An­fangs­zeit t₀ gleich 0 sind.

Formeln für Geschwindigkeit, Weg und Zeit bei konstanter Ge­schwin­dig­keit

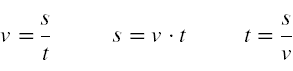
Achtung auf die Einheiten:

Die Einheiten müssen stets zusammen­passen! Um eine Geschwindig­keit 5, die in km/h gegeben ist, in g/s umzu­rechnen, divi­diert man die Geschwindig­keit einfach durch 3.6:

$$v = eighteen\ km/h \Rightarrow \frac{eighteen}{three.half dozen} \Rightarrow v = five\ \frac{m}{due south}$$

Umgekehrt geht man ähnlich vor: Multi­pliziert man eine Geschwindig­keit v in der Einheit m/south mit three.six, erhält man dice­selbe Geschwindig­keit in km/h:

$$5 = 10\ one thousand/s \Rightarrow x⋅3.6 \Rightarrow five = 36\ km/h$$

Alternative:

Setzt man den Weg in km und dice Zeit in h ein, bekommt human being die Geschwindig­keit in km/h.

Formeln für dice durch­schnitt­liche Be­schleu­nigung

Dice durch­schnittliche Be­schleu­nigung a (Englisch acceleration, daher die Abkürzung a), die Ge­schwin­digkeits­änderung v oder die benötigte Zeit t können mit den folgenden Formeln berech­net werden, wobei dice durch­schnittliche Be­schleu­nigung a konstant ist:

$$a=\frac{\Delta five}{\Delta t}=\frac{v(t_1)-v(t_0)}{t_1-t_0}=\frac{v_1-v_0}{t_1-t_0}=\frac{Geschwindigkeitsänderung}{benötigte\ Zeit}$$

$$\Delta five= a·\Delta t\qquad \Delta t =\frac{\Delta v}{a}$$

Bedeutung der Variablen

a	konstante durchschnittliche Beschleunigung in m/s² im Intervall [t0; tone]
Δv	Geschwindigkeitsänderung (= Geschwin­dig­keits­differenz) in m/s im Intervall [t0; tane]
Δt	benötigte Zeit (= Zeitdifferenz) in s (Englisch fourth dimension , daher die Abkürzung t)
five(t0) bzw. five0	Geschwindigkeit zum Zeitpunkt t0 (Anfangsgeschwindigkeit); v0 und t0 sind oft 0
v(ti) bzw. v1	Geschwindigkeit zum Zeitpunkt ti (Endgeschwindigkeit)

Hinweise zu den Formeln und speziell zu Differenzen

• Ein negativer Wert für die Beschleu­nigung bedeutet, dass tat­sächlich gebremst bzw. verzögert wird.
• Den folgenden Formeln liegt die obige Definition der durch­schnittlichen Be­schleu­­nigung bzw. dessen Integral zu­grunde. Dice Geschwin­dig­keit zum Zeitpunkt t₀ wird als Anfangs­geschwin­digkeit v₀ be­zeichnet und dice Ge­schwin­dig­keit zum Zeit­punkt t_i als End­ge­schwin­dig­keit v.
• Die Zeit­differenz Δt und die Weg­differenz Δs werden ver­ein­facht durch t bzw. s darge­stellt. Sind s(t₀) und t₀ gleich 0, kann man jedoch ignorieren, dass es sich bei Weg und Zeit eigent­lich um Differenzen handelt. Ein Anfangs­weg s₀ ist in den Formeln also prinzipiell nicht berück­sichtigt, da er für die meisten Auf­gaben nicht relevant ist. Homo kann aber den Weg southward durch den Term s – s₀ ersetzen, wie dieses Bei­spiel nach den Formeln zeigt.
• Weiter unten finden Sie ein weiteres Bei­spiel mit der Berechnung einer Zeit­differenz.

Werbung

Formeln bei gleichmäßiger Beschleunigung – Anfangs­geschwindig­keit = 0

Diese Formeln gelten für eine konstante Be­schleu­nigung bzw. Ver­zögerung, wobei sowohl die Anfangs­ge­schwindig­keit als auch der Anfangs­weg null sein müssen.

Im Prinzip sind das die gleichen Formeln wie im folgenden Abschnitt, nur dass dice Anfangs­ge­schwindig­keit 5₀ gleich null gesetzt wird. Dice 5. Zeile ent­fällt aufgrund der fehlenden Anfangs­geschwin­dig­keit v₀ kom­plett.

Beachten Sie den Hinweis zu den Differenzen im vorigen Abschnitt!

Formeln für eine Anfangsgeschwindigkeit gleich 0 bei konstanter Beschleunigung.

Bedeutung der Variablen

v	Endgeschwindigkeit in m/s
five0	Anfangsgeschwindigkeit in one thousand/south
a	Beschleunigung bzw. Verzögerung in thousand/south²
south	zurückgelegter (Brems-)Weg (= Differenz der Wege) in thousand
t	benötigte Zeit (= Differenz der Zeiten) in s

Formeln bei gleich­mäßiger Be­schleu­ni­gung – An­fangs­geschwin­dig­keit ≠ 0

Die nachfolgenden Formeln gelten nur für eine gleich­förmige (= kons­tante) Beschleu­nigung bzw. Ver­zögerung (= Bremsen, negative Be­schleu­nigung) mit einer möglichen Anfangsge­schwindigkeit ungleich 0 . Beachten Sie den Hinweis zu Differenzen ! Zur Bedeutung der Variablen siehe dice vorige Tabelle!

Formeln zur Berechnung von Bremsweg, Beschleunigung, (Anfangs-)Geschwindigkeit und Zeit für eine Anfangsgeschwindigkeit ungleich 0; Voraussetzung: konstante Beschleunigung.

Beispiel mit Anfangsweg southward₀

Ist ein Anfangsweg gegeben, wird in der Formel für den Weg (1. Zeile, 3. Spalte) southward durch s – due south₀ ersetzt. Anschließend bringt man s₀ auf die andere Seite, um den gesuchten Weg s zu erhalten:

$$southward=\frac{a}{ii}·t^ii+v_0·t\Rightarrow s-s_0=\frac{a}{2}·t^ii+v_0·t\Rightarrow s=\frac{a}{ii}·t^2+v_0·t+s_0$$

Einfaches Beispiel

Dieses Beispiel zeigt, dass obige Formeln durch­aus auch in der Praxis anwend­bar sind. Man benötigt nur eine Uhr mit Sekunden­anzeige oder eine Stopp­uhr, die auf jedem Smart­phone vor­handen ist, und ein Maß­ring.

Angabe

Ein Gartenbahnzug fährt um 16:ten:05 ab und chapeau um 16:10:11 seine Höchst­geschwindig­keit erreicht. Er legt dabei einen Weg von nine m zurück. Unter der Vor­aus­setzung, dass die An­fangs­geschwindig­keit 0 one thousand/s beträgt (Beschleu­nigung aus dem Still­stand) und die Be­schleu­nigung konstant ist, ist

• dice benötigte Zeit,
• die durchschnittliche Beschleunigung,
• die End­geschwindig­keit und
• die durch­schnittliche Geschwindig­keit zu berechnen.

Berechnung der Zeit

Die für den Beschleu­nigungs­vor­gang benötigte Zeit ist die Differenz der beiden Uhr­zeiten:

$$11 – 5 = half-dozen \Rightarrow t = 6\ s$$

Berechnung der Beschleu­nigung

Einsetzen in dice Formel in der 2. Zeile, letzte Spalte liefert dice ge­suchte Beschleu­nigung:

$$a = \frac{2⋅southward}{t^two} = \frac{ii⋅ix\ m}{(6\ s)^2}\Rightarrow a = 0.5\ m/s^two$$

Berechnung der Endge­schwin­dig­keit

Nun kann man sich leicht die Geschwin­dig­keit aus­rechnen, indem man ein­fach eine der drei Formeln aus der three. Zeile aus­wählt. Bei Ver­wendung der two. Formel erhält man:

$$five = a⋅t = 0.v\ m/s^two⋅6\ due south \Rightarrow five = 3\ thou/s$$

Will man die Geschwin­dig­keit in km/h wissen, ist five noch mit 3.half dozen zu multi­plizieren: iii⋅3.vi = 10.8 km/h

Berechnung der Durch­schnitts­geschwin­dig­keit

Da zum Zeitpunkt t = 0, also zu Beginn, der Weg 0 beträgt, braucht human being nur zwei Zahlen zu divi­dieren. Ein­setzen in die Formel five = south/t ergibt:

$$5 =\frac{9\ m}{6\ due south} \Rightarrow v = one.5\ m/s = 1.5⋅three.six\ km/h = 5.four\ km/h$$

Wie man sieht, ist die Durch­schnitts­geschwin­dig­keit nur halb so groß wie die End­ge­schwin­dig­keit.

Momentangeschwindigkeit & Momentanbeschleunigung

Ist die Beschleunigung bzw. Ge­schwin­dig­keit nicht kons­tant , ist die Ver­wendung der obigen Formeln unzu­lässig. Statt­dessen berech­cyberspace homo die Beschleu­nigung, die Geschwin­dig­keit oder den Weg per Differ­ential- oder Inte­gral­rechnung .

Dice wichtigsten Formeln

Die momentane Geschwindig­keit v(t) zu einem beliebigem Zeit­punkt t berechnet man durch ein­maliges Ab­leiten (Differenzieren) der Weg­funktion southward(t) nach der Zeit t (= Differ­ential­quotient ):

$$v(t)=\frac{d}{dt}southward(t)=\dot south(t)$$

Ist hingegen die momen­tane Beschleu­nigung bekannt, muss man die Beschleu­nigungs­funktion a(t) nach der Zeit t inte­grieren, um die Momentan­geschwin­dig­keit v(t) zu bekommen:

$$v(t)=\int a(t)dt$$

Dice Momentan­beschleunigung a(t) erhält human being durch ein­maliges Ableiten der Geschwindig­keits­funktion v(t) oder durch zwei­maliges Ableiten der Weg­funktion s(t) nach der Zeit t:

$$a(t)=\frac{d}{dt}five(t)=\dot v(t)$$

$$a(t)=\frac{d^2}{d^2t}south(t)=\ddot due south(t)$$

Den zurückgelegten Weg s(t) bekommt man durch Integration der Geschwindigkeit v(t):

$$due south(t)=\int 5(t)dt$$

Aus­führ­liche Infos, Her­leitung der Formeln für eine konstante Beschleu­nigung und Bei­spiele:

>> Zusammen­hang Ruck, Beschleu­nigung, Geschwin­dig­keit und Weg <<

Bedeutung der Variablen

v(t)	Funktion der Momentangeschwindigkeit in Abhängigkeit von t
southward(t)	Funktion des Weges in Abhängigkeit von t
a(t)	Funktion der Momentanbeschleunigung in Abhängigkeit von t
t	Zeit t in s

Werbung

Seite erstellt am eleven.07.2019. Zuletzt geändert am 26.05.2022.

Source: https://www.johannes-strommer.com/formeln/weg-geschwindigkeit-beschleunigung-zeit/

Posted by: williamscones1936.blogspot.com

Share this post